Bounding $R^2$

We have $X, Y, Z$, where $Z \sim X$ has $R^2=.1$ and $Z \sim Y$ has $R^2=.2$. Bound the $R^2$ of $Z \sim X + Y$.

Solution

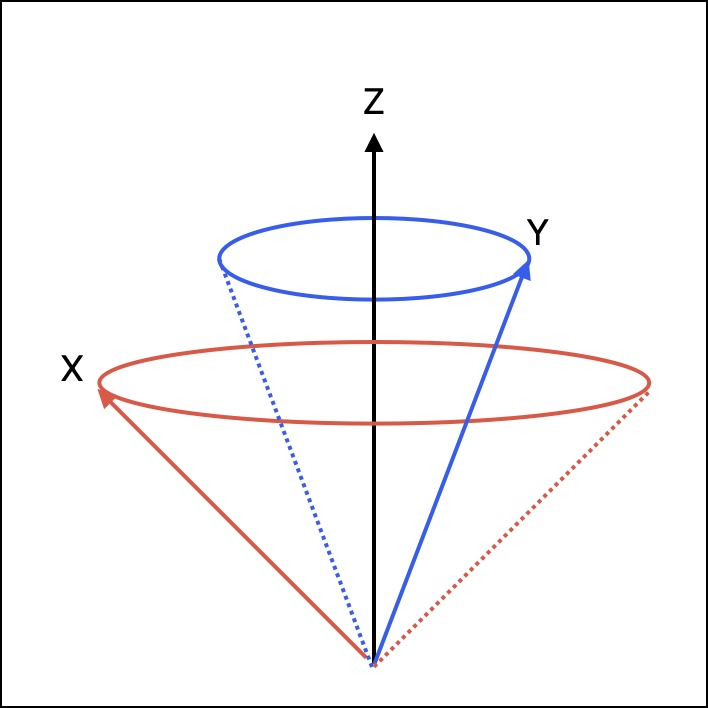
In linear regression questions, its important to remember the different ways to view linear regression: algebraically, geometrically, and statistically. In this case the geometric viewpoint is most fruitful. The class of all features that yield an $R^2=a$ lie on a cone around $Z$. So we know $X$ lies on one cone, and $Y$ lies on another cone, this one more tightly around $Z$.

Thus we can look at what placements of vectors on these cones results in the maximum and minimum $R^2$ (see image below). We reach a minimum of $R^2=0.2$ when the plane spanned by $X$ and $Y$ is orthogonal to the residuals of $Z \sim Y$. We reach a maximum when $Z$ is in the plane spanned by $X$ and $Y$, and thus the $R^2=1$.